出典
International Conference on Learning Representations 2019に採択。
所感
長くなってしまったので最初に所感を。
初めて読んだときはなんだかよくわからず挫折してしまったけど、4.2節あたりの気持ちをちゃんと読んでみると多少わかってきた。詳しい式変形はよくわからないままだがTD誤差と言いたくなるのはそうかもしれない。
確かにジャンプ予測は実現できたら面白いものの一つだと思う。しかし、Predictronとかもそうなのだけど、この手の環境モデルは時系列データの遷移を予測するだけで自分の行動を考慮できていないので、実践的には使い勝手が悪そう。結論の節で「プランニングへの応用を目指している」と書いてあるし当然こういった問題を認識していないわけはないが。
各タイムステップで行動選択が可能であると考えると、単純に状態系列に行動も含めれば上手くいくわけではないだろう。個人的には行動自体の表現を考えて抽象化することで漫然とした(長いタイムステップの)行動を考えられるようになるのではないかと考えているが。
将棋的に言うと「金銀を盛り上げていけば模様がよくなりそう」とか「飛車を振って美濃囲いにすれば勝ち」とかそういう方針的なものを……ってそれはむしろ階層的強化学習とかの分野なのかもしれない。どちらかというと「▲2四歩△同歩▲同飛△2三歩▲2九飛」を一気に飛ばせるとかそういう話か。しかしポリシーが偏っていれば1手ごとの展開でもそこまで計算時間のロスは大きくないだろうし、やはり観測が完全なドメインではあまり活きない話なのかもしれないとも思ったり。
概要
以下の3つの特徴を持つ環境モデルとしてTD-VAEを提案
- 状態の抽象表現を獲得
- 状態の不確実性を表現する信念を形勢
- 複数ステップ一気にジャンプする遷移を予測可能
1 Introduction
- 強化学習における部分観測環境
- 不確実性の表現が可能である必要性
- 記憶を持つエージェントならモデルフリー手法でも可能?
- 報酬のような教師信号では不確実性を学習するのは難しい/遅い可能性
- 望ましい性質
- データの抽象的な状態表現を学習し、観測レベルだけでなく状態レベルで予測
- ある時点までの観測値を全て考慮した符号(信念状態)を学習
- 複数ステップを一気にジャンプする予測が可能
- これらの要求を満たすものとしてTD-VAEを提案
2 モデルに要求されること
2.1 隠れ状態空間の構築
自己回帰モデル
- チェインルールを用いたモデル化
$$ \log p(x_1, \dots, x_T) = \sum_t \log p(x_t | x_1, \dots, x_{t - 1}) $$
- RNNを用いると隠れ状態
でデータに文脈を付与して予測を行うことになる
- 観測空間でそのまま予測をするのでデータの圧縮した表現を学習できない
状態空間モデル
潜在変数を用いて状態間の確率的遷移をモデル化
を状態系列、
を観測系列としたとき同時確率を次のようにモデル化
$$ p(\boldsymbol{x}, \boldsymbol{z}) = \prod_t p(z_t|z_{t-1})p(x_t|z_t)$$
- 事後分布
による下限によって学習(VAEと同様)
を、
をフィルタリング、平滑化する関数とすると事後分布は自己回帰的に分解可能(これ自明? よくわからなかった)
$$ q(\boldsymbol{z}|\boldsymbol{x}) = \prod_t q(z_t | z_{t - 1}, \phi_t(\boldsymbol{x})) $$
- 変分下限(よくわからん。VAEの式変形を調べないとダメそう)
$$ \log p(\boldsymbol{x}) \ge \mathbb{E}_{\boldsymbol{z}\sim q(\boldsymbol{z}|\boldsymbol{x})} \left[ \sum_t \log p(x_t|z_t) + \log p(z_t | z_{t-1}) - \log q(z_t | z_{t-1}, \phi_t(\boldsymbol{x})) \right] $$
2.2 信念状態のオンライン生成
- 過去の系列は十分な表現力を持つ変数
によって近似できるとする
$$ p(x_{t+1}, \dots, x_{T}|x_1, \dots, x_t) \approx p(x_{t+1}, \dots, x_{T}|b_t ) $$
RNNだと隠れ状態
が
に相当
状態空間モデルでは潜在変数
を媒介
$$ p(x_{t+1}, \dots, x_{T}|x_1, \dots, x_t) = \int p(z_t|x_1, \dots, x_t) p(x_{t+1}, \dots, x_{T}|z_t) dz_t $$
上の式と同様に
と近似できるとする
古典的な状態空間モデルではこのような
は考えられてこなかった
- 事後分布を自己回帰的に計算する
と、
の周辺事後分布に関するいくらかの不確実性がサンプル
にリークする可能性がある(とは?)
- サンプルは確率的なので、
に関する全ての情報を
から得るために、
を再サンプリングする必要がり、順々に
から
まで再サンプリングする必要がある
- (この2点が何を言わんとしているのかあまりよくわからなかった。なんとなく
を考えた方が良さそうという気分は読み取れたが……)
- 事後分布を自己回帰的に計算する
3 系列TD-VAEのための信念状態ベースELBO
- 状態空間モデル
を考える
- 目標はデータの対数尤度
最大化
- 自己回帰的に分解して
- 所与の
に対して、条件付き尤度
を
と
で条件付け
- 尤度の変分下限は
- 自己回帰的に分解して
$$ p(x_t| x_{\le t}) \ge \mathbb{E}_{(z_{t-1}, z_t) \sim q((z_{t-1}, z_t)|x_{\lt t})} \left[ \log p(x_t|z_{t-1}, z_t, x_{\lt t}) + \log p(z_{t-1}, z_t | x_{\lt t}) - \log q(z_{t-1}, z_t | x_{\le t}) \right] $$
- ここで
- 状態空間モデルにはマルコフ性が仮定されるので
かつ
を自己回帰的に分解して
- 状態空間モデルにはマルコフ性が仮定されるので
$$ \therefore p(x_t| x_{\le t}) \ge \mathbb{E}_{(z_{t-1}, z_t) \sim q((z_{t-1}, z_t)|x_{\lt t})} \left[ \log p(x_t|z_t) + \log p(z_{t-1} | x_{\lt t}) + \log p(z_t|z_{t-1}) - \log q(z_t|x_{\le t}) - q(z_{t-1}|z_t, x_{\le t}) \right] $$
と
は時刻が異なるだけ
を
に対する信念状態の符号として
で近似
- 同様に
の平滑化事後分布を
として表現
- 最終的に損失関数は
$$ -\mathcal{L} = \mathbb{E}_{z_t \sim p_B(z_t|b_t), z_{t-1}\sim q(z_{t-1}|z_t, b_t, b_{t-1})} \left[ \log p(x_t|z_t) + \log p_B(z_{t-1}|b_{t-1}) + \log p(z_t|z_{t-1}) - \log p_B(z_t|b_t) - q(z_{t-1}|z_t, b_{t-1}, b_t) \right] $$
4 TD-VAEと飛躍状態モデリング
4.1 TD-VAEモデル
- 離れた2つのタイムステップに対応するために3章で示したものを改良
- モデルの全体図
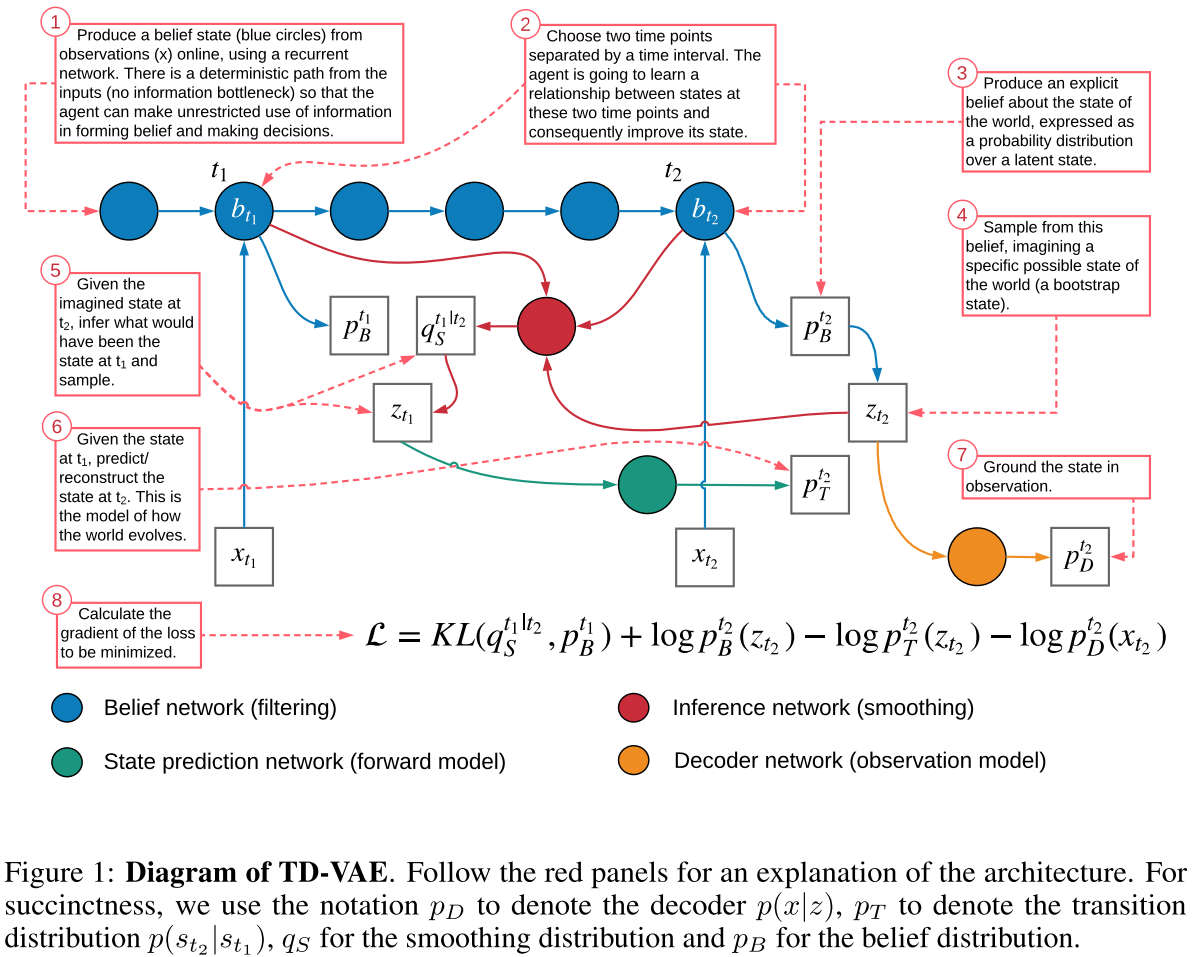
- 損失関数は前章の
が
に、
が
に置き換わって、
$$ -\mathcal{L}_{t_1, t_2} = \mathbb{E}_{ (z_{t_1}, z_{t_2}) \sim q(z_{t_1}, z_{t_2} | b_{t_1}, b_{t_2}) } \left[ \log p(x_{t_2}|z_{t_2}) + \log p_B(z_{t_1}|b_{t_1}) + \log p(z_{t_2}|z_{t_1}) - \log p_B(z_{t_2}|b_{t_2}) - q(z_{t_1}|z_{t_2}, b_{t_1}, b_{t_2}) \right] $$
4.2 TD-VAEの直感的背景
時間までに得た全ての情報から将来の時刻
の状態を予測したいとする。時間
までの観測情報は
に圧縮されている。また観測
の背後にはマルコフ性を満たす隠れ変数
があるとする。
今時刻がであるようなエージェントを考える。このエージェントは信念モデル
からサンプリングすることによって隠れ状態を推測することができる。状態
は観測値
を伴うはずなので、まず
を最大化したくなる(損失関数第1項・再構成誤差)。そして
を通じて
の情報がリークしすぎないように変分ボトルネックペナルティとして
を最大化したくなる(損失関数第4項・気持ちはわかる気がするが、この定式化が正しいのかはわからない。意味合い的には尖りすぎないようにする効果が出る? 式変形で出てきた者に対する解釈ということなのだろうか。あと論文中では第2項と書いてあるけど第4項だと思う)。
そしてにおける状態が
における状態から予測できて欲しい。まず
における状態がなんであったのかを予測する必要がある。これは単に
を使って求めるよりも
の情報を使った方が良い予測ができそう。よって
という平滑化分布を考えてこれにより
を予測する。この
を用いてジャンプモデル
を最大化する(損失第3項)。
最後に平滑化分布とだけで求めた分布の距離を最小化する(これがTD誤差っぽい部分だと思う)。多分平滑化分布の方が良い予測ができるはずで、それを
だけから求められるようになると嬉しいので。これは
と
のKL距離を考えて展開すると
(第2項と第5項)が出てきそう(だけど正確にはよくわからない。
を
について積分するはずだけどそれは上手く消えるのかな)。
これらの損失の和を考えると上のような式になっている。
4.3 TD学習との関係
強化学習だと状態について収益の分布を考える。多くの場合、状態価値や行動価値として収益の期待値だけを近似する。場合によっては収益の分布そのものを近似しようとすることもある(Categorical DQNなど)。
TD-VAEでは収益ではなくて状態の分布を近似することになる。
時点における状態を
における予測値でブートストラップ的に学習するので時間差分(Temporal Difference)的な学習である。
5 実験
5.1 部分観測ミニパックマン
- 実験内容:自分自身の周囲
しか見えないパックマン(の表示を簡単にしたやつ)において観測系列をモデリング
- 比較手法
- フィルタリングモデル:
- 平均場モデル:
- TD-VAE(ジャンプなしの連続モデル)
- フィルタリングモデル:
- 評価指標
- ELBO(低いほど良い)
- テストセットにおける負の尤度(低いほど良い)
- 結果

- 平均場モデルが最も性能が悪く、つまりただ単に
を信念状態として扱うだけでは性能が悪化することがわかる。TD-VAEによる工夫を導入することで
を正しく信念状態として扱うことができるようになる。
5.2 ムービングMNIST
- 実験目的:ジャンプ予測が可能であることの実証
- 実験内容:横移動するMNISTの画像を予測
- 手法時刻
からロールアウトした結果を出力
- 時刻
までの観測から
を計算
-
を
からサンプリング
-
から始めて
によって
の系列を取得
-
によって
の系列から
を復元
- 時刻
- 結果
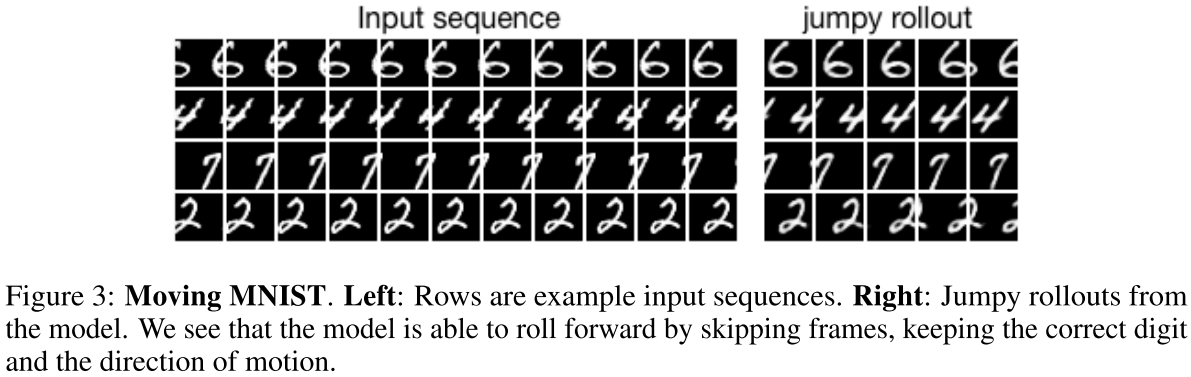
5.3 ノイズ付き調和振動子
- 実験目的:観測の情報が少ない場合でも状態予測が可能であることの実証
- 実験概要:ノイズの多い
- 階層的TD-VAEを利用
- 集約部分で積んだLSTMを使う?
- 結果
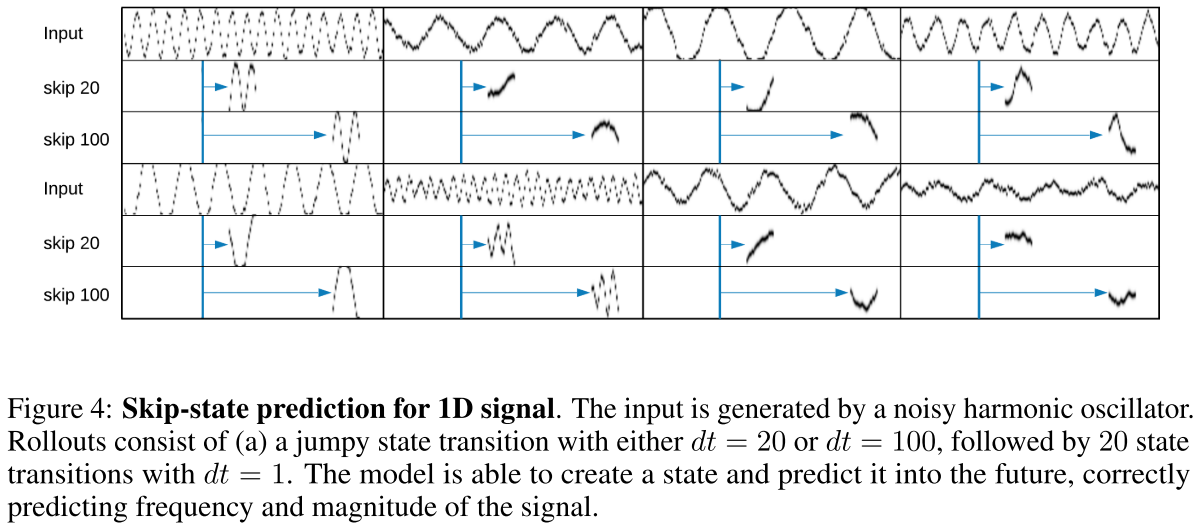
5.4 DeepMind Labでの実験
- 実験目的:より複雑なドメインでの性能検証
- 実験概要:DeepMind Lab環境において画像のジャンプ予測を実行
- 各モジュールにCNNを用いたモデル(Figure 8)を使用
- 実験1:最初に3つの
をサンプリングし、これらとこれらからジャンプした後の潜在変数を復元
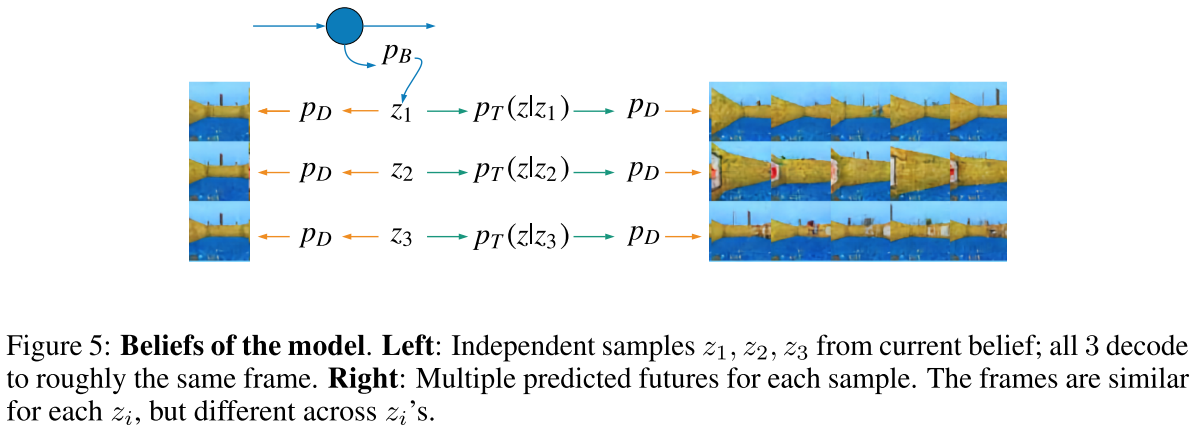
直接復元では
はどれも同じように見えるが、遷移した後の状態は異なる
- 見かけの観測の背後にある状態の違いを認識できている
実験2:ロールアウトの実験

- 複数ステップのジャンプ予測を行っても回転や前進の遷移を上手く捉えられている