結果
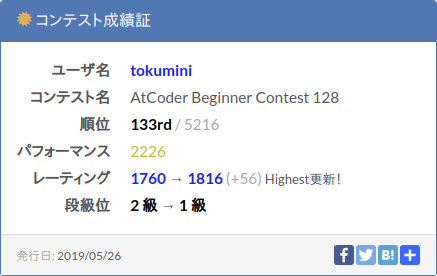
E問題までの5完で311位。パフォーマンスは1832でレート変動は1752→1760(+8)だった。E問題を解けてそこそこかなと思ったけど、パフォーマンスは思ったより低かった。慣れている人にとってはFが簡単だったらしいという影響もあったのかもしれない。
普通にif文で分岐。coutを並べるのがダサく思えるお年頃なので三項演算子を使いたくなってしまうが、3つ以上に分かれるときは混乱しがちなのでこれでいいと思う。
#include"bits/stdc++.h"
using namespace std;
using ll = int64_t;
int main() {
ll A, B;
cin >> A >> B;
if (A <= 5) {
cout << 0 << endl;
} else if (A <= 12) {
cout << B / 2 << endl;
} else {
cout << B << endl;
}
}
語ることなし。
#include"bits/stdc++.h"
using namespace std;
using ll = int64_t;
int main() {
ll r, D, x;
cin >> r >> D >> x;
for (ll i = 1; i <= 10; i++) {
x = r * x - D;
cout << x << endl;
}
}
パッと見で「左端の最大値と右端の最小値だけ考えれば良い」と判断したけど確信が持てなくて理屈を考えているうちに少し時間がたって、WA出てから考えようということで証明しきれないまま提出。負になる場合にそのまま出力してしまっていたので1WA。すぐ気づいて修正できたけど、ジャッジが詰まっていたりしたらちょっとまずかったかも。
#include"bits/stdc++.h"
using namespace std;
using ll = int64_t;
int main() {
ll N, M;
cin >> N >> M;
vector<ll> L(M), R(M);
for (ll i = 0; i < M; i++) {
cin >> L[i] >> R[i];
}
ll ans = *min_element(R.begin(), R.end()) - *max_element(L.begin(), L.end()) + 1;
cout << max(ans, (ll)0) << endl;
}
とりあえず問題文を読んだ段階で順番は関係なさそうと思ったので配列も操作列もソートして、あとは小さい方から貪欲に処理していって良さそうという感覚を信じて出して通った。std::pairの使用をすぐ避けてしまう。
#include"bits/stdc++.h"
using namespace std;
using ll = int64_t;
int main() {
ll N, M;
cin >> N >> M;
vector<ll> A(N);
for (ll i = 0; i < N; i++) {
cin >> A[i];
}
struct Op {
ll B, C;
};
vector<Op> ops(M);
for (ll i = 0; i < M; i++) {
cin >> ops[i].B >> ops[i].C;
}
sort(A.begin(), A.end());
sort(ops.begin(), ops.end(), [](Op& lhs, Op& rhs) {
return lhs.C > rhs.C;
});
ll index = 0;
for (const Op& op : ops) {
for (ll i = 0; i < op.B; i++) {
if (A[index] < op.C) {
A[index++] = op.C;
} else {
break;
}
}
}
cout << accumulate(A.begin(), A.end(), (ll)0) << endl;
}
制約を完全に
と勘違いしていた。それだと
の\という制約もとんでもないことになるんだけど、そこも見間違えていて
で解く問題だと思い込んで解いていた。
まず2駒の配置だけを考えて最終的にそれを
倍すれば良いということにはすぐ気づく。なので2駒の配置についてのコストの和を
で求める問題だと思った。しかしこれが結構難しい。
2駒について片方の駒を固定してもう片方の駒を自由に動かすと、固定している方の上下左右について「「公差1の等差数列の和」を公差とする等差数列の和」を考えれば式が立つ(合ってるかは知らない)。
つまり片方を固定した場合については
で求まることはわかったが、固定するマスの位置を全探索すると
なので制約の勘違いによりダメだと思い込んでいた。
なんとかして計算量を落とすフェーズに入る。理屈から言えば上の式を展開してなんやかんや公式をぶちこめば総和自体もで求められそうだが上の式を展開するのは地獄なのでやりたくない。こういう場合はたいてい差分計算すればなんとかなると信じて、固定マスを列方向に1ずらしたときを考えていく。
すると直前までいた列までの数字は全て+1になって、それより右は全て-1になることに気づく。つまり今
列目にいるとすると
が差分になる。差分がに関する1次式になっているので、回ずらしたときの値はに関する2次式になる。それの総和を求めることは二乗の総和を計算する公式をググってで計算可能。
結局一番下の式(
が抜けていて
を足す数が1回少ないので正確には
)を計算すればよい。駒が左端にいるときの初期値だけは頑張ってで求めれば、それを右にずらしていった結果もこの式でで求まるので、後は初期位置を各行についてで考えれば良い。
2駒について各位置関係を2回足しているので2で割って、あとは倍して、ようやく答え。結構難しいと思ったんだけど、ただの制約見間違えだったとは……。
#include"bits/stdc++.h"
using namespace std;
using ll = int64_t;
constexpr ll MOD = 1e9 + 7;
ll MODpow(ll n, ll m) {
ll result = 1;
while (m) {
if (m % 2 == 1) {
result *= n;
result %= MOD;
}
m /= 2;
n *= n;
n %= MOD;
}
return result;
}
int main() {
ll N, M, K;
cin >> N >> M >> K;
ll ans = 0;
for (ll i = 0; i < N; i++) {
ll tmp = 0;
ll x = 0;
(x += i * (i + 1) / 2 % MOD) %= MOD;
(x += (N - i - 1) * (N - i) / 2 % MOD) % MOD;
ll sum = M * (M - 1) / 2 % MOD;
ll sum_u = ((sum + M - 1) + (sum + i * (M - 1))) * i / 2 % MOD;
ll sum_d = (sum + (sum + (N - i - 1) * (M - 1))) * (N - i) / 2 % MOD;
(x += sum_u) %= MOD;
(x += sum_d) %= MOD;
(tmp += M * x % MOD) %= MOD;
ll pow2 = (M - 1) * M * (2 * M - 1) / 6 % MOD;
(tmp += N * pow2 % MOD) %= MOD;
ll sub = (M - 1) * (M - 1) * M / 2 % MOD * N % MOD;
tmp = (tmp + MOD - sub) % MOD;
(ans += tmp) %= MOD;
}
(ans *= MODpow(2, MOD - 2)) %= MOD;
for (ll i = 0; i < K - 2; i++) {
(ans *= N * M - 2 - i) %= MOD;
}
for (ll i = 1; i <= K - 2; i++) {
(ans *= MODpow(i, MOD - 2)) %= MOD;
}
cout << ans << endl;
}
本番中はE問題で時間と体力を奪われたのもあってあまりまともに考察できなかった。中央値を見ればよいというのにも気づいていなかったし、中央値はpriority_queue2本で管理できるという話も知らなかった。解説PDFを読んで、確かにそんな感じで解けそうということで適当に書いて通した。AtCoderしかやってないとこういう典型？ があんまり身についていない説がある？ よくわからないけどこういう問題が出てくれるならそれはそれで楽しい。
#include"bits/stdc++.h"
using namespace std;
using ll = int64_t;
int main() {
ll Q;
cin >> Q;
priority_queue<ll> left_pq;
priority_queue<ll, vector<ll>, greater<>> right_pq;
left_pq.push(LLONG_MIN);
right_pq.push(LLONG_MAX);
ll sum_b = 0;
ll min_v = 0;
for (ll i = 0; i < Q; i++) {
ll op;
cin >> op;
if (op == 1) {
ll a, b;
cin >> a >> b;
sum_b += b;
if (left_pq.size() == right_pq.size()) {
if (a < left_pq.top()) {
min_v += left_pq.top() - a;
}
if (a > right_pq.top()) {
min_v += a - right_pq.top();
}
} else {
min_v += abs(left_pq.top() - a);
}
if (a >= right_pq.top()) {
right_pq.push(a);
} else {
left_pq.push(a);
}
if (right_pq.size() > left_pq.size()) {
left_pq.push(right_pq.top());
right_pq.pop();
} else if (left_pq.size() > right_pq.size() + 1) {
right_pq.push(left_pq.top());
left_pq.pop();
}
} else {
cout << left_pq.top() << " " << min_v + sum_b << endl;
}
}
}
を定数として扱い、その値を2.5としたもの
