Mambaの周辺知識(2) Parallel Scanの逆伝播・状態空間モデルの離散化

　前回はParallel Scanのforwardについてある程度確かめた。今回はParallel Scanの逆伝播と状態空間モデルの離散化について確認する。

Parallel Scanの逆伝播

【2024/05/04】理解に誤りがあった部分の記述を訂正。

　mamba.pyにおいてParallel Scanの逆伝播はpscan_revという新たな関数を用いて実装されている。これは「flip the input, call pscan, then flip the output」を行う操作とのことである。これで上手く計算できることを系列長4の場合を手計算して確かめる。

　まず順伝播を振り返ると、結局出力する値は長さ4では

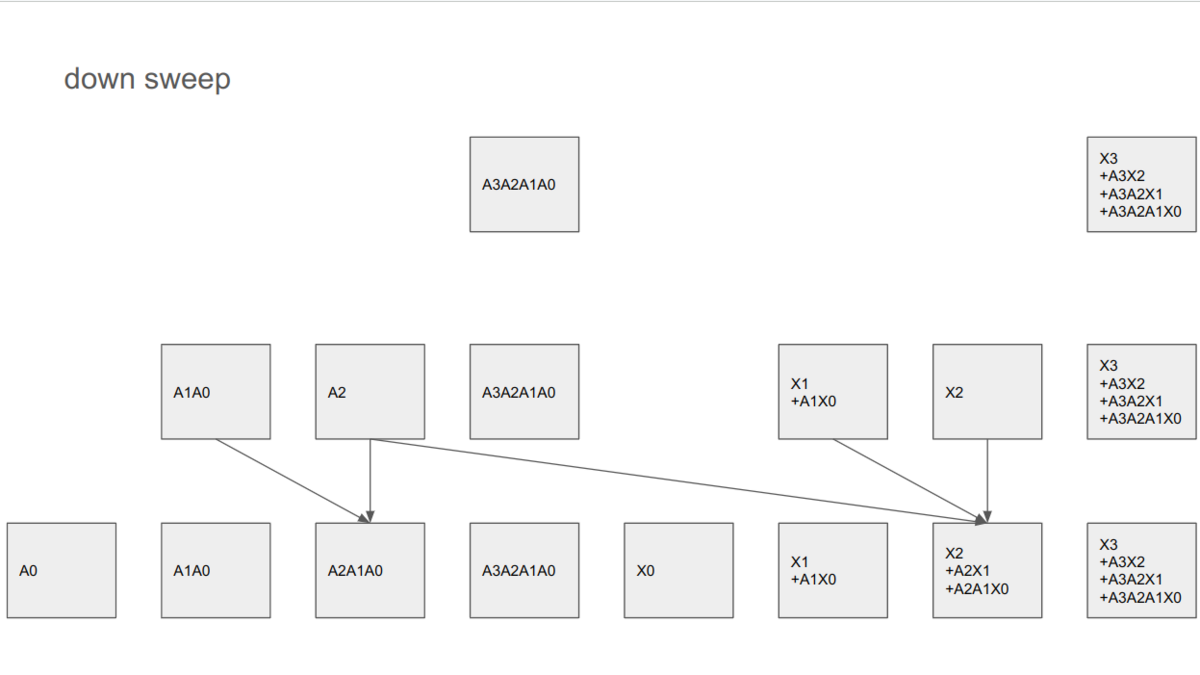
となるのだった。これの右半分に相当する部分が次の層に渡される。逆伝播ではそれぞれの要素に相当する勾配 $G _ 0, G _ 1, G _ 2, G _ 3$ がやってくるので、 $A$ および $X$ についての勾配を求めれば良い。偏微分して

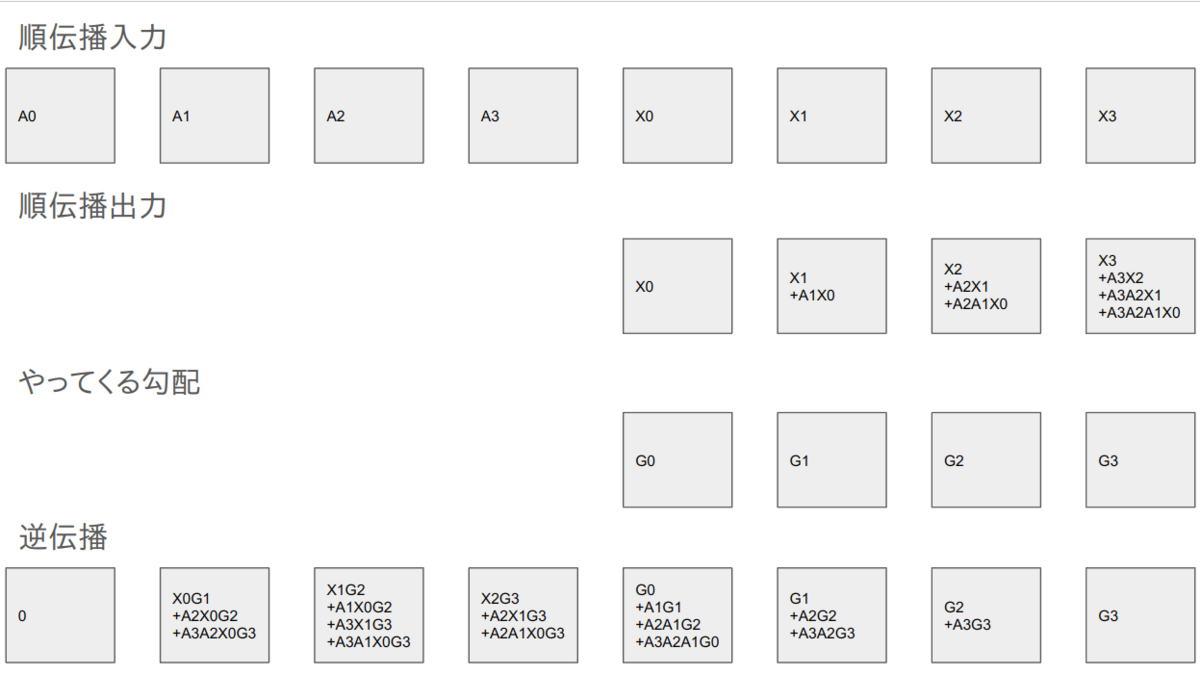
ということになる。右半分の $X$ に対応している勾配は綺麗な形をしているので順伝播の形と照らし合わせれば「flip the input, call pscan, then flip the output」であることが見えてくる。（ただし $A$ のインデックスを一つずらす必要があることに注意）

　左半分の $A$ の方はやや複雑だが、順伝播時の結果の $X$ と、勾配をpscan_revしたものを上手く要素積を取るということになる。

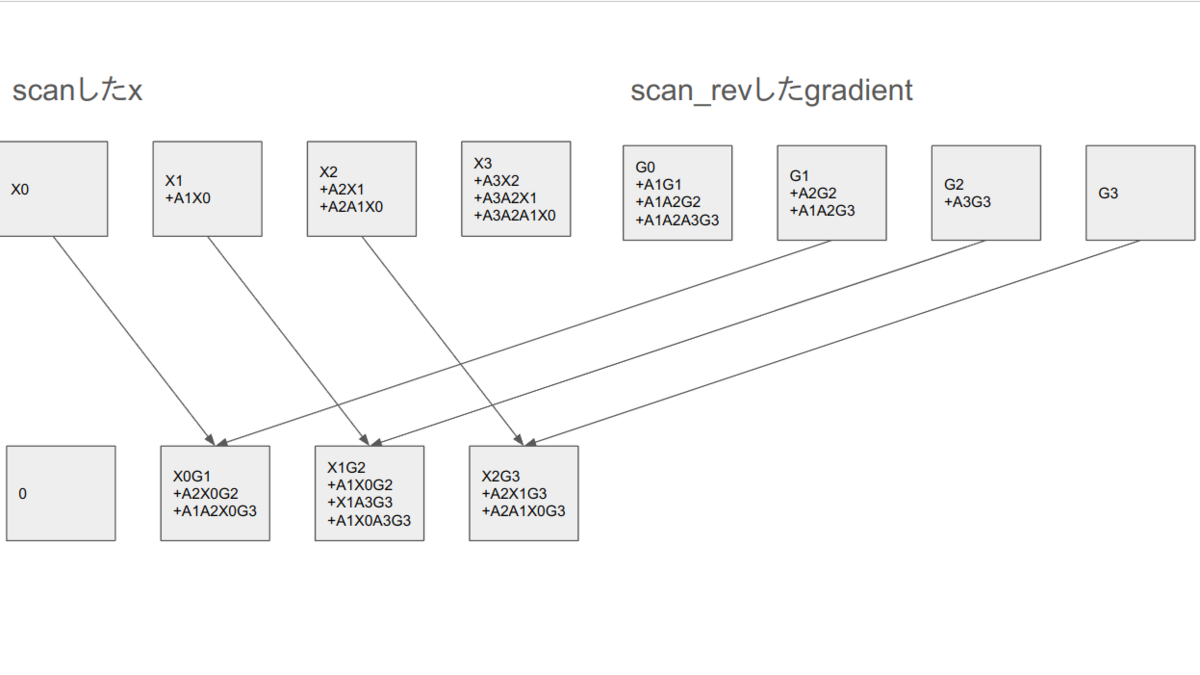
　結局mamba.pyが実装している通りでやれそうだということが確かめられた。もちろんこれを長さに対して一般化してちゃんと定式化する必要はあるが、直観的にはこのような操作でできることがわかった。

状態空間モデルの離散化

　参考：zero-order hold | studywolf

　（参考というか上記リンクをほぼ写しただけ）

　まず微分方程式を整理する。微分方程式の操作としては基礎的なもののような気がするが、自分はこのあたりの理解が浅いので丁寧に式変形をする。

$\dot{x}(t) = A x(t) + B u(t)$

について

$\dot{x}(t) - Ax(t)= B u(t)$

とまとめて、眺めていると両辺に $e ^ {-A t}$ をかけたくなる。というのも積の微分で左辺が

$e ^ {-A t} \dot{x}(t) - e ^ {-A t} A x(t) = \frac{\partial}{\partial t} \left( e ^ {-A t} x(t) \right)$

と変形できるからである。つまり

$\frac{\partial}{\partial t} \left( e ^ {-A t} x(t) \right) = e ^ {-A t} B u(t)$

であり、両側を積分して

$e ^ {-A t} x(t) = e ^ 0 x(0) + \int _ 0 ^ t e ^ {-A \tau} B u(\tau) d \tau$

となり、 $e ^ {-A t}$ を払って

$x(t) = e ^ {A t} x(0) + e ^ {A t} \int _ 0 ^ t e ^ {-A \tau} B u(\tau) d \tau$

が得られた。

　ここから離散化のためにさらに整理する。以下ではとりあえず等幅の場合としている。本質的に等幅でないと成り立たない式変形はないと理解しているので、Mambaのように可変にすること自体は問題ないはず。タイムステップ幅を $T$ とすると $k$ 個目の時間は $kT$ であり、これに対応する値を $x _ k$ と書くと

$x _ k = e ^ {A k T} x(0) + e ^ {A k T} \int _ 0 ^ {kT} e ^ {-A \tau} B u(\tau) d \tau$

となる。 $x _ {k + 1}$ のことも並べてみる

$x _ {k + 1} = e ^ {A (k + 1) T} x(0) + e ^ {A (k + 1) T} \int _ 0 ^ {(k+1)T} e ^ {-A \tau} B u(\tau) d \tau$

右辺第一項が上手く消えるようにすることを考えると

$\begin{align} x _ {k + 1} - e ^ {AT} x _ k &= e ^ {A (k + 1) T} \int _ 0 ^ {(k+1)T} e ^ {-A \tau} B u(\tau) d \tau - e ^ {A (k + 1) T} \int _ 0 ^ {kT} e ^ {-A \tau} B u(\tau) d \tau \\ &= e ^ {A (k + 1) T} \int _ {kT} ^ {(k+1)T} e ^ {-A \tau} B u(\tau) d \tau \end{align}$

　ゼロ次ホールド（Zero Order Hold）というのは要するに各区間で入力を一定値とみなすということだけの話らしい。つまり $t \in \lbrack kT, (k+1)T \rbrack$ で $u(t)$ が定数ということになる。

$\begin{align} e ^ {A (k + 1) T} \int _ {kT} ^ {(k+1)T} e ^ {-A \tau} B u(\tau) d \tau &= e ^ {A (k + 1) T} \int _ {kT} ^ {(k+1)T} e ^ {-A \tau} d \tau B u _ k \\ &= \int _ {kT} ^ {(k+1)T} e ^ {A \left((k+1)T - \tau \right)} d \tau B u _ k \end{align}$

ここで、指数を積分の中に組み込んだのは変数変換をしたいからで、 $v = (k +1)T - \tau$ を考える。そうすると $\frac{\partial v}{\partial \tau} = -1$ で、 $\tau = kT$ のとき $v = T$ 、 $\tau = (k+1)T$ のとき $v = 0$ なので

$\begin{align} \int _ {kT} ^ {(k+1)T} e ^ {A \left((k+1)T - \tau \right)} d \tau &= \int _ {T} ^ {0} e ^ {Av} dv \\ &= -\int _ {0} ^ {T} e ^ {Av} dv \\ &= A ^ {-1} e ^ {Av} | _ {v=0} ^{T} \\ &= A ^ {-1} (e ^ {AT} - I) \end{align}$

（Aが行列の場合は逆行列が存在するとする）

　以上をまとめて

$\begin{align} x _ {k + 1} = e ^ {AT} x _ k + A ^ {-1} (e ^ {AT} - I) B u _ k \end{align}$

が得られた。