Value Prediction Networkを読んだ際のメモ

論文

出典

　Thirty-first Conference on Neural Information Processing Systems (NeurIPS 2017) に採択。

　※この記事の図は全て論文中のもの

概要

  • 抽象表現での遷移を予測して内部的にプランニングを行うValue Prediction Networkを提案
  • 短い先読みでもDQNを上回っているので良い表現を獲得できている可能性

1. Introduction

  • 次の観測情報を直接予測するモデル（Observation-Prediction Model）は観測情報の次元数が大きいときや遷移が確率的なとき困難
  • 生の観測情報は意思決定について不要な情報（背景など）が含まれる
    • 本当に欲しいものは次の観測情報ではなく価値→Value-Prediction Modelである必要

2. Related Work

　省略

3. Value Prediction Network

3.1 アーキテクチャ

　 \boldsymbol{x}が観測、 \boldsymbol{s}が状態表現、 \boldsymbol{o}がオプション（行動）としてVPNは次の4モジュールを学習

f:id:tokumini:20191028153752p:plain

　これらを用いて次のようにRollout

f:id:tokumini:20191028153943p:plain

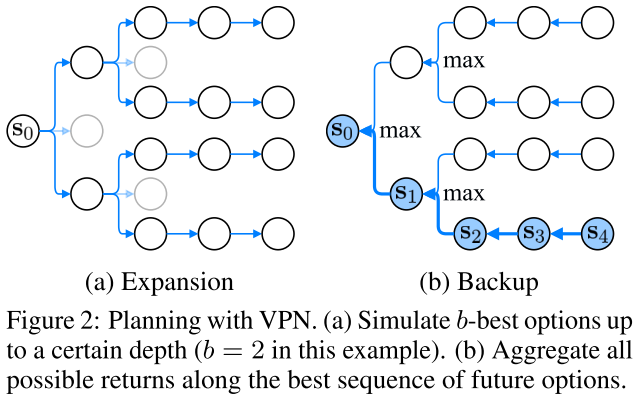
3.2 プランニング

  • 理論上MCTSとかもできるが今回は簡単なプランニング手法を利用
  • 深さ dまで上位 b手のみを展開してゲーム木を構築して、バックアップ時には現在の状態の価値と最善値を混ぜて返す
f:id:tokumini:20191028154407p:plainf:id:tokumini:20191028154421p:plain

3.3 学習

　nステップTD法のような形で行う。 \epsilon-greedy方策で軌道を生成し \boldsymbol{x}_t, \boldsymbol{o}_t, r_t, \gamma_t (1 \le t \le n + 1)を得る。時刻 t時点での損失は、3.2のように kステップのロールアウトを行った結果がどれも現時点での教師信号に合うように設計する。

$$ \mathcal{L}_t = \sum_{l = 1}^{k} (R_t - v_t^l)^2 + (r_t - r_t^l)^2 + (\log_\gamma \gamma_t - \log_\gamma \gamma_t^l)^2 $$

　ただし $$ R_t = \begin{cases} r_t + \gamma_t R_{t+1} & \mathrm{if}\; t \le n\\ \max_\boldsymbol{o} Q_{\theta^{-}}^d (\boldsymbol{s}_{n+1}, \boldsymbol{o}) & \mathrm{if}\; t = n + 1 \end{cases} $$ であり、 Q_{\theta^{-}}^d (\boldsymbol{s}_{n+1}, \boldsymbol{o})は固定したターゲットネットワークを利用して3.2における深さ dの探索を行う値。

3.4 他手法との関係

　VPNは価値の推定に抽象状態遷移を利用するという意味ではモデルベースに近く、しかし結局価値を重視して価値の推定を行うことが目的という点でモデルフリーと見なすこともできる。トレーニング中に先読みを用いて高精度な教師情報を生成できるため、通常のQ学習よりも収束が速い。

4. 実験

　主に検証する内容は次の三つ

  1. VPNはDQNのようなモデルフリーのベースラインを超えるか？
  2. Observation-basedなプランニングと比べたVPNの利点とは何か？
  3. VPSはAtariゲームのような高次元で敏感な入力を持つ難しいタスクに対して有効か？

4.1 実験設定

ネットワークアーキテクチャ
  • Encode : CNN
  • Transition : Optionごとに異なる1層CNN,差分を予測
  • Outcome : Optionごとに異なる1層CNN + 2層全結合層
  • Value : 2層全結合
実装詳細
  • n-step Q学習を16並列で実行
  • 10Kステップごとにターゲットネットワークを同期
  • VPN特有のハイパーパラメータ
    • 学習における予測ステップ k
    • 学習における探索深さ d_{train}
    • 評価における探索深さ d_{test}
      • 明示しない場合 k = d_{train} = d_{test}としVPN( k)として表記
    • 探索時の枝分かれ量 b:深さ3までは4,それ未満は1
  • 比較手法として次の状態表現ではなく観測値を予測してプランニングするOPN( k)を用意

4.2 収集ゲームにおける実験

タスクの説明

f:id:tokumini:20191028180908p:plain

　見下ろし型2D迷路において、青いマスにできるだけ多く到達するタスク。各エピソード20ステップで、青いマスに到達すると+2.0、各時間ステップで-0.2の報酬を得る。観測情報は \mathbb{R}^{3\times 10 \times 10}の形式であり、加えて[0,1]の範囲に正規化された残り時間を連結した3次元テンソルが入力となる。通常の確定的環境に加えて、各青いマスが0.3の確率で1ブロック移動し、0.3の確率で同じ行動を複数回繰り返すことができる確率的環境でも実験した。

結果

f:id:tokumini:20191028181327p:plain

  • DQNより高性能
  • OPNは確率的環境で性能悪化するがVPNは良い
    • OPNは観測の期待値を予測しがちで、それを入力とした価値関数が期待値を出力するとは限らない
  • 探索深さが増えるほど性能が向上する
汎化性能

　学習した環境とは異なるようなゴールが少ない（8→5）環境（FGと呼ぶ）、壁が多い環境（MWと呼ぶ）でも性能を検証

f:id:tokumini:20191028182306p:plain

　やはりVPNの汎化性能が良い。

テスト時の探索深さ

f:id:tokumini:20191028182445p:plain

　学習時の探索深さが小さいとテスト時の探索深さを増やしたときに悪影響が出るが、探索深さ3以上で学習していればほぼ問題はない。そして探索深さは5だが学習中に10ステップ予測を行うもの（VPN(5)*）では性能は上がっていった。

4.3 Atariゲーム

  • 10ステップに渡って同じ行動を取り続ける
  • ゲーム画面は84×84のグレースケールに処理して4フレームを入力とする
  • 割引率は固定し、3オプションステップ先までの予測を行う（実時間的には0.5秒先まで）

f:id:tokumini:20191028183057p:plain f:id:tokumini:20191028183107p:plain

　性能が高く、学習も速い。たった3ステップ分の予測でも性能が良くなっていることから、表現学習に良い影響を与えた可能性がある。

f:id:tokumini:20191028183318p:plain

　実際に予測した行動系列を可視化してみても良さそうな予測に高い価値が割り当てられている。

所感

　Transition部分の損失は明示的には組み込まれておらず、数ステップ先の価値を予測することで間接的に学習されることが期待されているのみのようだ。きっぱりしていてすごいが、状態の予測（環境モデルの学習）というよりは価値を予測する際の補助という意味合いが強いのかもしれない。

　適用ドメインも（おそらく）全部一人ゲームだと思うので、これをボードゲーム等に適用するとどうなるかはわからない。探索深さもあまり深くはないし、（実験ドメインの性質かもしれないが）Figure7を見るに探索を増やしてもすぐ頭打ちになっているところはやや気になる。

　遷移して画像レベルで再構成することは難しいし無駄が多いという感覚はあるが、一方で表現ベクトルまでいく前の「何がどこにある」というレベルでの特徴は正確に遷移が予測できて欲しいとも思う。そういう特徴抽出もニューラルネットワークがやっているわけなので難しいところだが、遷移の予測がいくらか補助タスクとして表現学習に有用そうだという結果がちらほら出ている感じなのは悪い材料ではなさそうだ。

　個人的には、遷移を考えるために有用な特徴と良さを判断するうえで重要な特徴は、重なりがありつつも全く同じではないと思われる。いくらか浅い層の部分で遷移を考えてそこから何層か加えて表現を深めて価値を推定するという形などを考えてみたいところだが果たして。